取材・写真・文／大草芳江

2011年3月4日公開

1948年、大阪府出身。専門は結晶成長学。1975年、東北大学大学院理学研究科修士課程修了 （理学博士）。1979年、ナイメーヘン大学（オランダ）研究員、1981年、IBMチューリヒ研究所客員研究員、Phillips研究所(オランダ、アインドーヘン)客員研究員、1983年、東北大学大学院理学研究科地球物質科学科助手、助教授などを経て、2006年から現職。

　「科学って、そもそもなんだろう？」を探るべく、【科学】に関する様々な人々をインタビュー
科学者の人となりをそのまま伝えることで、「科学とは、そもそも何か」をまるごとお伝えします

「結晶成長」を"ものさし"として、地球や宇宙でのさまざまな現象を理解しようとする、
塚本勝男さん（東北大学大学院理学研究科教授）に聞くインタビューシリーズの第２弾。

一見すると、専門分野とは関係がないこと、日常生活でのちょっとした疑問、
それら一つひとつを「不思議だな」と考えて、大切にしていく塚本さん。

しかし、それら一つひとつは、まるで小さな結晶のように、いくつもの形となって集まり始める。
そして、やがて大きな結晶となるように、最終的には一つの強いアイディアへと結び付いていく。

「一つひとつのことを馬鹿にせず、大事にすべきだよね」と語る、
塚本さんという「人」から見える、科学とはそもそも何かを探った。

＜目次＞
・宇宙での"その場"観察装置のヒントはパリの空港にあった
・結晶に縞模様はなぜできる？
・すべての対流を抑えて、均一な結晶をつくることに初めて成功
・パリ空港での記憶が、宇宙基地における装置の基本原理に
・ちょっとしたことでも不思議だと思っていると、いずれは役に立つ
・今の科学でも金平糖は不思議
・金平糖のつくり方
・金平糖づくりは３つのステージに分けられる
・問題はなぜツノが出るのか？
・ツノの数はどうやって決まる？
・形を見ることでその歴史がわかる
・形を理解することは、すべてを理解すること
・粒子の大きい結晶に注目が集まっている
・粒子の大きな結晶はつくるのが難しい
・学問が加速度的に進歩するとき
・いろいろな考えがだんだん整理され、一つの強いアイディアに結び付いていく

宇宙での"その場"観察装置のヒントはパリの空港にあった

　ちょうど先日、ベルギーのブラッセルで、アメリカのNASA、ヨーロッパのESSA、日本のJAXAの皆さんと一緒に、今後の宇宙実験について話し合う会議に参加しました。

　その帰り、パリのシャルル・ド・ゴール空港を久しぶりに訪れて、ちょうど思い出したんですよ。宇宙での"その場"観察の大きなヒントは、実はそこから来ているんだってね。

―シャルル・ド・ゴール空港と宇宙での"その場"観察装置（※）、一体どんな関係があるのですか？

（※塚本さんが"結晶成長"をものさしにして地球や宇宙での様々な現象を理解しようと開発した高分解光学法による結晶成長"その場"観察法のこと。宇宙を原子・分子のレベルで観察できるこのユニークな装置は、欧米で評判となり、国際宇宙ステーション等での結晶成長"その場"観察装置の基本となった。詳細は、第１回インタビューをご覧ください）

　シャルル・ド・ゴール空港は、昔から非常に斬新なスタイルの空港なんです。僕が初めてヨーロッパを訪れた約２０年前、シャルル・ド・ゴール空港の長いエスカレーターの天井に、直径３０ｃｍくらいの球が約１０ｍ間隔で吊るされていました。その球に色々な宣伝がスライド投影される広告の仕組みです。僕はそれをボケっと眺めて、おもしろいなと思ったんです。

―どのあたりがおもしいと思ったのですか？

　例えばスクリーンに投影する場合、普通なら平面に投影するでしょう？もし球面に投影すれば、球面のあるところはピントが合うけれども、あるところではピントが合わない。

　でもパリの空港の宣伝では、球面全体にピントが合っていたのです。それはなんでだろう？と思ったわけですね。別に技術的には難しくないのだろうけど、僕はそれを非常に新鮮に感じて、それが宇宙での"その場"観察のきっかけの一つになったんですよ。

―ピンボケせずに球面全体に投影できる理由をどのように考えたのですか？

　普通の写真撮影でも、ピントが合うところと合わないところがあるよね。それを利用すると、どこでも球面の表面にピントが合うような絵をフィルムに収めることができると思ったわけね。ま、当たり前と言えば当たり前なのだけど。

　けれども、そこが重要なんです。従来の"その場"観察を考えてみると、結晶の表面の図を綺麗に撮ることはされていたし、我々もしていました。というのは表面というのは、非常に平らだったからですね。けれども球の表面についてはなされていなかったのです。

結晶に縞模様はなぜできる？

―球面表面が重要になる場面はあるのですか？

　例えば、実際に宇宙実験で使ったのは結晶ではなく、結晶になる前の液体なんです。液体が宇宙でどう挙動するのか。世界中でいくつかのグループが研究していました。

　その研究のために「液柱」という液体の柱をつくるのです。液柱の表面でどんな流れが起こるかを研究するのも、一つのテーマだったわけです。

―「結晶」と「流れ」、どんな関係があるのですか？

　急に「流れ」というと不思議に思うかもしれないね。じゃあ、その前にまずは、この写真を見てみて。結晶をつくって断面を見ると、こんな縞模様ができるんです。

【図１】結晶内部の縞模様

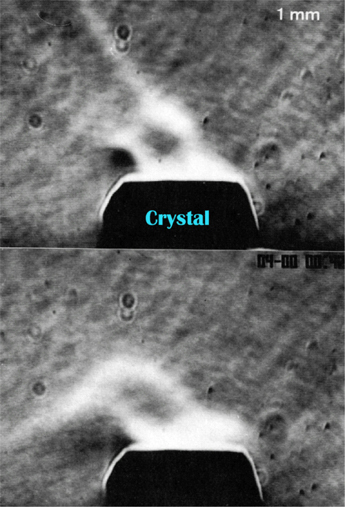
【図２】不安定な対流

―なぜ縞模様ができるのですか？

　結晶が溶液中で成長する時、そのまわりの濃度が下がると、薄くなるから軽くなる。すると浮力が生じて、浮力でもって流れが生じる。時間とともにフラフラしているわけね。

　ということは、結晶のまわりの濃度が時間とともに変わっているから、結晶の成長速度が速くなったり遅くなったりを繰り返すのです。すると樹木の年輪のように、縞模様ができるのですよ。でも、縞模様があると困るんです。

―なぜ縞模様があると困るのですか？

　例えば、シリコン半導体をつくるときに縞模様があると、電気抵抗が場所によって変わったりするので困るわけですね。そこで、この縞模様をなくす研究が盛んに行われました。その結論として、このような不安定な対流がその原因である、ということを皆さんが考えるようになったんです。

すべての対流を抑えて、均一な結晶をつくることに初めて成功

　ならば、流れのない宇宙で実験してみれば良いのでは、ということで、ドイツ人研究者のベンツさんらのグループが実験したわけです。予想では、宇宙だったら重さがないから、対流なんて起こるはずない。だから、縞模様はできるはずではなかったんですね。

―結果はどうだったのですか？

　ところが実験をやってみると、結果として縞模様ができちゃった。それで、なんでだろう？といろいろな人が考えたんですね。流れの原因は、重さだけじゃなかった。そして結論として「表面張力流（マランゴニ対流）」の話を持ち出したのです。

―「マランゴニ対流」とは、どのような流れなのですか？

　例えば、お粥の表面に薄い膜ができるけれども、膜はずっと引っ張られるよね。あれは重さで引っ張られているのではなくて、お粥の表面がつくる表面張力が液体の表面を引っ張っているわけです。そのような流れがあることが、当時わかり始めていた頃でした。

　つまり、それが重さがなくても縞模様ができることの原因だ、ということを皆さんが言い出したわけです。重さの対流はないけど、液体の表面があって、その表面張力の差（勾配）があると、温度勾配や濃度勾配と同じようにして、流れが生じる。

　要するに、表面張力が大きければ、それがお粥の表面みたいに引っ張るわけですよね。宇宙で流れが起こる原因は、そのようなマランゴニ対流じゃないか、ということを考えたわけです。だったら、やっぱり実証しないとだめだ。けれども、どうやって実証する？

―「宇宙は表面張力が支配する世界だ」と第１回目のインタビューで伺いました。
　宇宙では、重力の効果は消せても、表面張力の効果を消すことはできないのでは？

　マランゴニ対流を宇宙でどうやって止めるか？と言うと、これは重さをなくしたとしても、消すことはできません。そこで、シリコンの液柱の表面を、別の流れにくい液体で包んでしまったわけですよ。

　そうすれば、流れやすい自由表面がないから流れは起きにくいだろう、ということだね。そして実際に、その２～３年後、スペースシャトルで実験をしたのだけれども、予想通り、初めて縞模様がなくなったというわけなんだ。

　つまり、初めてマランゴニ対流を抑えることによって、すべての対流を抑え、均一な結晶をつくることに成功したわけです。

パリ空港での記憶が、宇宙基地における装置の基本原理に

　ま、それはあくまで結果なんですよね。けれども、本当にマランゴニ対流が止まっているのか？どれくらいの速度でマランゴニ対流が起こるか？を見ようとすると、液体の表面を見れば良いわけ。でも液体の表面は円柱だよね。だからピントが合わない。

―あ、そこで最初の話とつながるのですね。

　そう。パリのシャルル・ド・ゴール空港で見た、直径約３０ｃｍの球に投影したスライドの光学系。その原理を使えば、円柱だって別に怖くないよ。円柱の表面を地図のように引き延ばしたような図は見えるはずだ。

　例えば写真を撮る時でも、どこでもピントが合うように、レンズを絞り焦点深度を深くするのも一つのテクニックだよね。けれども、それでは解像度を落としているわけね。一方、レンズの絞りを開くとシャープにはなるけど、ピントが合うところは限定されてしまう（焦点深度は浅い）。

　けれども僕らは科学者として、高解像度で撮ろうとするから、絞りを開いた状態で撮りたいのです。そのためには、球面をちゃんと平面に直せるようなレンズをつくっておけば済むことだ、ということがわかったわけ。考えれば当たり前のことなんだけどもね。

―今までそのようなレンズはなかったのですか？

　今までそのようなレンズはなかったのだけど、オリンパスがちゃんとつくってくれたんだね。これが、日本で最初の宇宙実験、特に流体のマランゴニ対流が起こるシーンを撮る装置の基本になったわけです。

　それでもって初めて、マランゴニ対流が起こるきっかけについて、例えば温度差をつくるとマランゴニ対流が起こりますよとか、いろいろな実験ができるようになったわけですね。

　そうやって、この装置の基本的な考えは、１９９１年の日本の小型ロケット「ＴＲ－１Ａ」１号機に初めて採用され、現在の宇宙基地の実験装置に受け継がれているのです。

　つまり、２０代の頃に記憶に残っていたものが、そのまま現在の宇宙基地の一つのスタイルになった、というわけだね。その時に同時につくったのが、第１回のインタビューで話した、結晶成長の"その場"観察装置なんですよ。その装置も、２０代の頃の記憶が原型であるということだね。

ちょっとしたことでも不思議だと思っていると、いずれは役に立つ

　やっぱりね、ちょっとしたことでも「不思議だ」と思っていると、いずれは役に立つことがあるんだね。それを先日、パリの空港を訪れてちょうど思い出したんです。でも、もうあの球形の広告はなかったけどね。僕はあれ、フランスらしくて良いと思うんだけどな（笑）

―第１回のインタビューでも、小さな頃から身近な現象に対して不思議だなと思っていたことが基本となって、ある時に不思議だと思ったこととつながっていき、だんだん大きなサイエンスになっていくプロセスを伺いました。

　そうなんだよね。小学校の頃、プラモデルをつくっていたのだけど、既製品だけでなく木からもつくって、そこで必ず工夫をするんだね。それが今でも必ず生きている。そういった教育って、あっても良いのだよねぇ。

　実際、小中学生から２０歳頃までに考えたことで今も飯を喰っている、と言っても過言ではないと思いますよ。もちろん技術的には確かに高度になっているし屁理屈をつけているかもしれないけど（笑）。でもモチベーションは、そんな時からできているんじゃないかな。

　さて、"その場"観察の二本柱のうち、第１回目のインタビューでは、主に結晶成長の話をしました。第２回目となる今回は、流体の話でした。特にマランゴニ対流をどう観測するかの基本的なことは、そこで決まったということです。それが１９９１年くらいのことですね。

　流体の詳しいことは専門家ではないので、"その場"観察装置は彼らに預けました。その後も、日本で発達して、今の宇宙基地の実験装置になっていると思います。

今の科学でも金平糖は不思議

　ところで今回、本当は宇宙の話をしようと思っていたのだけど、やっぱり今、盛んにやっている金平糖の話をすることにしました。金平糖は昔から不思議に思われていたんですよ。

―なぜ金平糖なのですか？

　今でこそ金平糖は日本の伝統的な菓子ですが、そもそもは１６世紀頃、ポルトガル人が鉄砲と一緒に日本に持ち込んで伝わった、と言われています。織田信長が砂糖菓子として食べていたのが金平糖なんですよ。

　ポルトガルでこの前、「ポルトガルに金平糖はあるか？」と皆に聞いてみたところ、「ない」と言っていましたね。つまり現在、金平糖は日本にしか残っておらず、日本で独自に発展してきたのです。

【図３】金平糖

　金平糖というのは、結晶と同じように形が不思議なんですよ。結晶や鉱物を調べる人は、常にその色や透明度などを見るのですが、そのほかに形がすごく綺麗ですよね。形が綺麗と言えば、雪の結晶もそうです。

　雪の結晶は、平板状から樹枝状のものまで、皆千差万別の形を持っています。どうしてこんな形になるんだろう？それは結晶を扱う人なら必ず疑問に思うわけなんですね。

　結晶の話はいずれまたするとしても、結晶...まぁ砂糖も結晶なのですが、金平糖の角（ツノ）は昔から皆さんの興味の対象なわけです。

―金平糖のツノは今の科学でも不思議なのですか？

　そうなんです。例えば、不思議なところはこういうところですよ。金平糖のツノはいくつあるかを、まず数えてみました。（これは秘書さんが一生懸命数えてくれたものです）

【図４】金平糖のツノの数を数えたようす

　機械で手軽につくる安価な金平糖のツノの数は、だいたい１６個くらいでした。一方、職人さんが丹念に手からつくる高価な金平糖のツノの数は、１８～２４と多様性はありますが、だいたい最大２４個くらいなんです。

　では、なぜそんなにシステマティックな数のツノになるのだろう？ということが、やっぱりおもしろいんですよ。やっぱり皆さんも興味を持つ対象なわけです。論文もいくつかあるんですよね。

金平糖のつくり方

　その前にまず、金平糖のつくり方を知っている？実は僕も、一月前までは知らなかったのですが。

―実際に見たことはないですが、鉄板でくるくる回しながら煎っていく、というのは聞いたことがあるような気がします。

　それは安価につくる方だね。一方、本格的に金平糖をつくれる職人さんは、おそらく日本に一人しかいないと思うけど、最初の種として「イラコ」を使うの。もち米を煎って粉にしたようなものだね。

　昔は「ケシの実」を使ったのです。あんパンの表面についている粒々がケシの実だよ。ケシの実を電子顕微鏡で見ると、こうなっているんです。

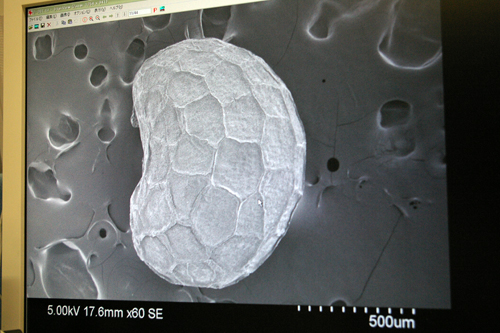
【図５】電子顕微鏡で見たケシの実の表面

　ケシの実はセル状になっていて、水を非常に吸いやすいの。きっとポルトガル人がつくった当時は、ケシの実だったのでしょうね。

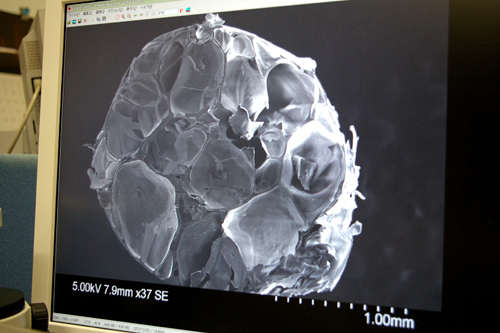
【図６】電子顕微鏡で見たイラコの表面

　一方、今の日本で使っている「イラコ」を電子顕微鏡で見ると、こんな感じです。非常に多孔質で水を吸うようなやつだね。ケシの実と何だか似ているでしょう？昔の人は、電子顕微鏡で調べたわけではないけど、経験的にそうしたわけですね。

【図７】右がイラコ、左がケシの実

　このイラコを大きな鉄板でずっと煎りながら、砂糖水をちょっと加えて、しばらくまた煎る工程を何度も２週間くらい繰り返すんです。そこにすごいテクニックが必要であることは、断面を調べることによって、だんだんわかってきました。

―鋳型で作っているわけではないのに、なぜこんな風にツノが出るのか不思議ですね。

　そう。問題はなぜツノが出るのか？ということなんですよ。先ほど最初の種として、イラコまたはケシの実を使うと話しましたが、もっと安価な金平糖は、サイコロ状のグラニュー糖を使うんです。このグラニュー糖を使った金平糖で１・２・３日後、どこからツノが出るかを調べた研究者がいるんですね。

　グラニュー糖でできた金平糖を割ってみると、真中に白いところがあるのわかるかな？それがグラニュー糖なんです。そのサイコロの角（カド）からツノが出ている。グラニュー糖からつくると、１６個のツノが出るんです。

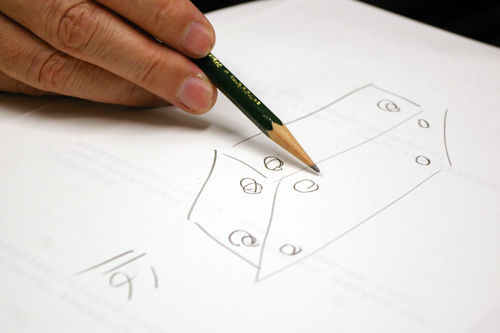
【図８】塚本さんが書いた図。グラニュー糖からつくった金平糖のツノの数は１６個。

　それを図に書いてみましょう。ツノは最初、サイコロ状のグラニュー糖のカドに近いところに出るんです。それを数えると、１，２，３，４，５，６，７，８，９，１０，１１，１２，１３，１４、１５，１６。全部で１６ですから、ツノの数と合いますね。

　ですから職人は、まず最初に何とかツノを出すようなことをして、それからツノが消えないように維持することによって、金平糖の形をつくることができる、ということがまず一つわかるわけです。

金平糖づくりは３つのステージに分けられる

　写真を見せながら説明しましょう。まず、真ん中に種となるグラニュー糖の結晶があります。グラニュー糖のカドのところからツノが出るような形。ですから職人としたら、最初に小さな結晶のツノをちゃんと出すことは、すごく大事な仕事なのでしょうね。

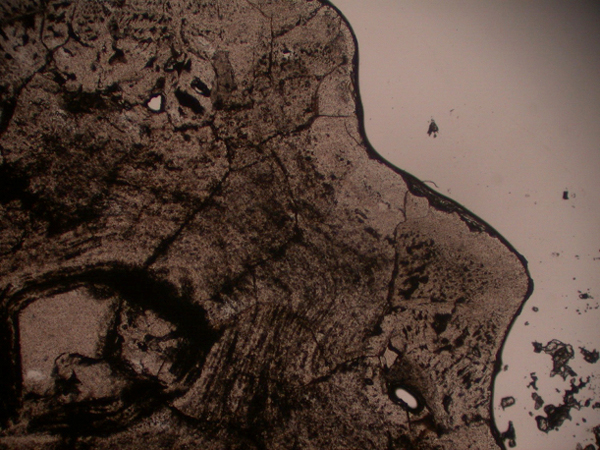
【図９】金平糖の断面写真。グラニュー糖のカドからツノが出ているようすがわかる。その後、グラニュー糖のカドから出たツノが消えないように受け継がれていく。

　もう一つ大事なことは、このツノが出たところから、ツノが消えないようにずっと受け継いでいくことです。受け継いでいるところを電子顕微鏡で拡大すると、小さな砂糖の微結晶の積重ねであることがわかりますね（小さいため黒く映っています）。

　さらに一つ拡大すると、この微結晶は、直方体（六面体）の砂糖の積重ねなのです。このように緻密な結晶が集まっているから、硬いのですよ。

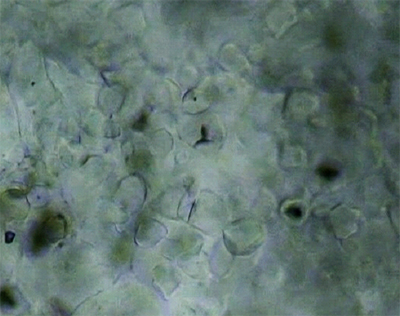
【図１０】グラニュー糖のカドから出たツノを拡大すると、直方体の砂糖の積み重ねであることがわかる。

　歯の硬さも同じ原理です。歯はアパタイトという結晶なのですが、一つの結晶ではすごくもろい。けれども小さな結晶がいろいろな方位に集まっているから硬いんですよね。

　そして最後の仕上げとして、表面にツヤをつくるために、蜜をかけて大きな結晶をつくるんです。多分あまり動かさないんでしょうね。このようにツノとツノの間に大きな砂糖の結晶ができるわけです。面を持った綺麗な結晶ができるからツヤがでるんですね。

【図１１】表面にツヤをつくるために大きな結晶がある。明るい部分が表面近くの結晶。右下が中心部。

　要するに、①ツノを出すステージ、②出たツノを維持しながら大きなツノに育てていくステージ、③最後に綺麗なツヤを出すために大きな結晶をつくるステージ。この３つのステージを、職人さんは経験的にやっているわけですね。

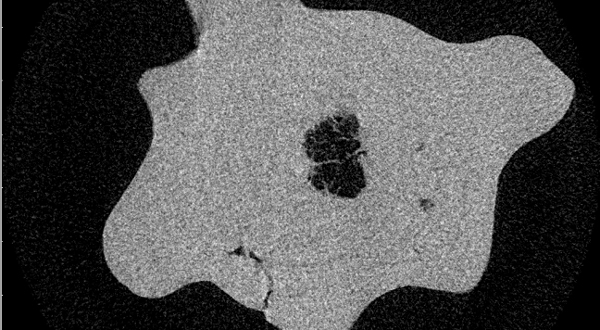
【図１２】エックス線CTによる金平糖の断片写真

　これは、エックス線CTによる金平糖の断層写真。これも貴重な写真です。真中にあるのはイラコ。けれどもイラコなのに、なぜかツノを持つような形ができる。そして、そこがツノが出るような形だということが、何となくわかるんだよね。

問題はなぜツノが出るのか？

―グラニュー糖はカドを持つけど、イラコは丸いです。なぜツノは出てくるのですか？それに、グラニュー糖でもツノが出てくる位置がカドから少しずれているのが気になります。

　問題はなぜツノが出るのか？ということなのね。そこ。ちなみにゴマの実は丸いから使えるかと思ったのだけど、ゴマの実では駄目でした。つるつるだから、水を含まないんですね。

　さっきの図で説明すると、このカドのところから少し離れたところに、ツノが出るんだよね。ちょうどカドに砂糖水がたまるのなら、何となくわかる。

　けれども、なぜこのカドのところから少し離れた位置に、砂糖水がつくかはわかりませんね。だから、ちょっと真面目に絵を書いて、蜜はどこにつくのだろう？と考えたの。

　まず最初に液がつくと、大抵カドに残りますよね。これは割とわかるんです。でも、なぜここ（カドから少し離れた位置）からツノが出るのだろう？を考えるために、では液がついたならば、その後どうなるか？を考えてみる。

―どのような考え方をするのですか？

　まず一番中間的なもの、つまり液と結晶の角度がちょうど４５度の時を考えます（図上）。もしこの角度が４５度よりも上ならどうなるか？を考えると、こうなっちゃうわけね（図中央）。そして４５度よりも下だと、こう切れてしまうよね（図下）。

【図１３】カドに液がついた後にどうなるかを場合分けして考えた図

　つまり、この結晶と砂糖水の濡れ角が４５度以下であるならば、ふたつに分かれる。濡れ角を支配するのは表面張力だから、それは要するに、表面張力次第だ、ということなのです。

　実際に、例えばこの結晶と砂糖水の間の角度を測ってみると、３０度以下なんだよね。すると必ずこうやって分かれるはずだ、ということを先日、実験したの。

　水滴をつけて、その水滴がどうなるかを調べたんです。砂糖ではできないので、例えば水晶で実験したり、コーヒーをカドのところにつけて、どのようにして液が表面のところに止まるかを調べたり、あるいは蒸発させたり。いろいろなことをやっています。

　すると結果的に、（最初にカドについた液滴は）二つに分かれています。つまり、液が大きければ、カドのところに来るのだけど、液が蒸発して小さくなるに従って、二つに分かれてしまうということ。

　よって、最初に誰かが統計的に調べていたように、このカドの少し離れたところで３つに分かれるようになるのが最も安定だ、ということがわかったわけです。

ツノの数はどうやって決まる？

　さあ、そうすると、だいぶわかってきましたね。まず、砂糖水はカドのところについた。でも、カドのところはやっぱり一番蒸発しやすいよね。なぜならば、サイコロみたいな結晶を鉄板で炒るわけだから、カドのところが熱くなって、そこが蒸発するから。

　だからますます、こういう風に液滴がついたら、すぐここ（カドから少し離れたところ）で結晶ができて、だんだんそこが育っていくのは納得できますね。

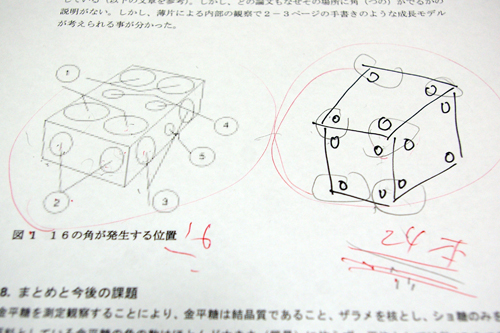
【図１４】１６のツノが発生する位置（左）と、２４のツノが発生する位置（右）

　では次に、なぜ高価な金平糖のツノの数は２４本か？ということね。単純に考えると、結晶が薄ければ、ツノの数は、１，２，３，...１０，１１，１２。それに裏面があるから、１３，１４，１５、１６の計１６個となるのね。では、結晶が厚くなったらどうか。１，２，３，...８、それが３×８＝２４。単純に２４という数字が出てくるわけですね。

　要するにカドに液滴が付く。けれども、それが表面張力、つまり濡れ角の影響で、面に分かれて３つに分かれる。だから、もともとの形が薄い板状なら１６個、厚ければ２４個だ、というように出てくるわけ。すると、うまい具合に説明できたなと思っているんです。

―グラニュー糖にはカドがありますが、炒り子にはカドがありません。それなのになぜ２４個の綺麗なツノが出るのですか？

　そこなんだよね。グラニュー糖ならツノの数は１６個、これはきれいに説明できるのです。じゃあ今度はケシの実や炒り子だったらどうなるのか？だって形を持ってないでしょう？ということなんだよね。

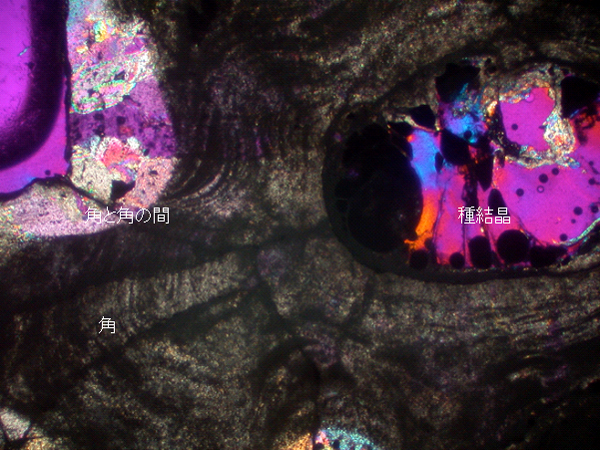
　だから、そのために金平糖の薄片をつくったの。イラコの断面も偏光顕微鏡で見える。イラコからツノが出始めたところから、どんどん引き継いでツノになり、最終的には仕上げのために透明になるでしょう？この三層が綺麗にできているんですよね。

【図１５】金平糖の断面写真（ＮＨＫ提供）

　さらにイラコの表面を拡大すると、表面に微細な砂糖の結晶が集合しているのが見えます。こういう結晶がだんだん育ってきて、イラコのまわりにツノができる。だからイラコのような形のものでも、尖っているところからツノが出るようになったことが、大体わかってきたんですね。

　ただ、なぜツノの数が２４に近づくか？ということは、まだよく説明できていません。けれども不思議なことに、小さな結晶がついている炒り子って、六角の直方体に近いような形になっていることが、だんだんわかってきているのですよ。

―最初は不定形だったイラコの形が、だんだん直方体になるのですか？

　そうそう。イラコが最初は不定形だと思っていたのだけど、そうじゃなくって、何となく面をもっているような感じに見えるよね。だんだん微細な結晶が集まって大きな結晶になる時、形が直線状の面で囲まれたようになってくる。だから、最大２４個のツノに近づくのは、理想的に言えば、おそらく大きな厚みのある直方体に近づくからだと思います。

　例えば天然の結晶でも、最初は小さな結晶がいっぱいくっついているわけね。けれども、だんだん大きな結晶になっていく。それと同じで、最初は砂糖の小さな結晶があったとしても、だんだん大きな結晶になる間に、何となく形が整ってきて、綺麗な面を持つようになる。そのカドがツノのきっかけになるんじゃないか？と、今は想像しているわけです。

　だから、職人技ってすごいよね。だって、イラコをうまく蒸発させて、ツノをちゃんと出して、それを２週間も維持させて、最終的にはツヤを出す。それって、すごい技術だよね、ということなんです。

【図１６】安価な金平糖の断面。大きな結晶粒でつくられており、崩れやすい。

【図１７】高価な金平糖の断面。３重構造で緻密。

　微細な結晶があるところは、サイズが小さいから見た目は真っ黒になるのね。反対に、大きな結晶のところは明るくなっています。これは安価な金平糖、これは高価な金平糖ね。ほら、三層構造になっている。

　それで、安価な金平糖はどうなっているか？と見てみれば、グラニュー糖のまわりは、どこも大きな結晶でしょう？だから、さくっと割れちゃうんです。

　けれども高価な金平糖は、まさに歯に近いよね。表面にエナメル質のようなものがある。だから硬いんだね。さらに、湿気があっても金平糖はベトベトしない。グラニュー糖の金平糖はベトベトするけどね。そういうことを職人さんは知らないうちにつくっているんだよね。

形を見ることでその歴史がわかる

　このようにして、種である結晶の形が、後々の結晶の形にまで影響を与えるという話は、ひとつの良い例かもしれないね。

―何の良い例なのですか？

　僕の得意分野は、結晶成長です。僕は砂川先生から学び、「結晶表面の成長パターンを見ることが大事」と教えられました。けれどもそれに対して「表面のパターンは、結晶成長の最終末期のパターンでしょう？その中の構造や、その中で成長していることのパターンは、それとは関係ないのでは」といった批判はよくあるわけです。

　僕らみたいに結晶成長中ずっと"その場"観察をするのなら問題ないです。けれども、例えば（結晶成長中をずっと見れない）天然の鉱物を拾ってきて、その鉱物の歴史を最終末期の表面だけ見て調べることができるか？と言えば、「それは最終末期だけで、中の構造や結晶ができた様子なんかは調べられないでしょう」という批判があるのですよ。

　けれども実はそうじゃなくて、結晶の外形は、中の状況や中の種の形を、引き継いでいるということなんだね。結晶表面のパターンだって、金平糖と同じで、種の形が後々の形に影響を与えることが、これでわかってきたわけなんですよ。

　理由がわかれば、中を何も調べなくても、ツノの数が１６個なら「あぁ、グラニュー糖を種に使ったな」、２４個なら「これは職人が丁寧につくったな」って、わかるわけでしょう？

　そのうち、形を見ただけで、その歴史がわかるわけ。人間でも「この形ができたのは、やっぱり甘やかされて育ったのか・そうでなかったのか」がわかるよね。それと同じことじゃないかな。そのような考えが、例えば天然の鉱物を調べようとするときも大事な話になるのではないでしょうか。

　つまり、その形やツノの形や数、こういったものができるのには、ちゃんとした理由がありますよ。その理由がちゃんとわかれば、どのような成長の履歴を辿ってきたかが、ちゃんと読みとれますよ、ということですよね。それが今回の結論なのではないでしょうか。

形を理解することは、すべてを理解すること

　例えば、鉱物でも何でもかんでも、すぐに溶かしたり潰しちゃったりして、分析しちゃうよね。けれども形だって、いろいろな情報を持っているのです。だから分析の前に形を見たいし、そういう目で調べるべきだと僕は思っている。

　まさに雪なんてそうですね。雪は溶かしたら水だし、氷も溶かしたら水です。けれども水を分析したって、雪だったか氷だったか、わからないでしょう？

　けれども形を見れば、これは雪だから空から降って来たんだ、これは氷だから水が凍ったんだ、とわかる。そういうところの情報というのは、すごく大事な話なんです。

　けれども一見、あまりにも単純過ぎるんだよね。形を見るなんて、そんなのサイエンスじゃない、と言うかもしれない。けれども、そうではなくて、形はすごいサイエンスなんです。

　例えば、温度データなどを測っても、それは非常に精密なデータを取っているかもしれないけど、あれは時間軸でとっているから１次元のデータだよね。でも、絵だったら二次元だし、形だったら３次元だよね。

　当然３次元の方がすごい情報を持っているわけです。ただ、まだどのような解析をすれば良いかがわからないから、何となく簡単な研究しかされていないのかもしれない。けれども形の研究をするということは、すべてを理解するのと等しいのではないでしょうか。

粒子の大きい結晶に注目が集まっている

　ところで、このオパールの色、ミステリアスで綺麗でしょう？これもシリカの微細な粒子でできている結晶で、いろいろ綺麗な色がつくんです。

―オパールの色って不思議ですね。

　そうですね。普通の結晶は、Ｘ線の波長のオーダー（1pm～10nm程度）で規則的に粒子が配列しています。それに対して、このオパールやコロイド結晶は、光の波長のオーダー（360～830nm程度：普通の結晶と比べて1000～1000000倍の大きさ）で粒子が並んでいるんです。

　このようなコロイド結晶は、他の結晶とは異なる性質を持っています。工学的に言えば「フォトニック結晶」とも呼ばれます。フォトニック結晶の性質を一言で言えば、色々な表現があるかもしれませんが、マイナスの屈折率を持っているということです。

　それによって、いろいろ不思議な性質が現れます。例えば、フォトニック結晶でレンズをつくると、どこでもピントが合うような光学系がつくれるとかね。今までの常識にはないような、様々な性質を持つのです。

　それは、まだ理論ができていないような光学系なんですね。ですから、宝石になるようなミステリアスなこの色は、まだ充分に説明できていないんです。

　でも、このようなフォトニック結晶をつくれば、例えば急速に光をそらすことができる電子デバイスなど、いろいろな電子デバイスをつくることができる。そのようなわけで今、物理学や工学の電子関係では相当の割合でフォトニック結晶の研究がされています。

粒子の大きな結晶はつくるのが難しい

　ただ難点は、あまりきれいに結晶をつくることができないことなんです。結晶成長は、小さな原子・分子の粒子の積重ねはできるけども、こんなに大きな粒子を綺麗に重ねていくことは、まだまだなかなかできないんですよ。

―なぜ難しいのですか？

　粒子が大きいと動きにくいので、例えば綺麗な位置に来るまでに別のやつが来たりして、乱れたりするんです。反対に、粒子が小さければ動きが早いので、綺麗な結晶になりやすい。

　つまり、小さな分子なら、結晶の表面にくっつく時、小さいので自由に回転しながら正規の位置にぴったりくっつくことができるわけです。

　けれども、大きな分子は回転もしにくいし、運ばれるのも難しいし、回転してその方位に合わせるのも難しい。だから大きな分子ほど、成長速度は非常に遅くなるわけですね。

　その中間に、タンパク質の結晶があります。タンパク質の結晶は、食塩や水晶やダイヤモンドなど普通の結晶と比べると、粒子の大きさが１０倍くらい大きいです。それでも、こういったものはやっぱり難しいですね。

　さらにタンパクの結晶よりも大きな分子に、例えばウイルスがあります。ウイルスはタンパクの分子よりもさらに１ケタ（１０倍）大きい。ウイルスも結晶になりますよ。結晶になるのだけど、大きいから運ばれにくいし、回転して方位を合わせることもできない。

―なぜ結晶化させる必要があるのですか？

　なぜ結晶化させるか？と言えば、大きな結晶をつくると、その分子の性質がわかるので、機能性がわかる。機能性を調べることで、例えばどんな薬として働くかを調べることができるわけね。

　なぜならば、一つの分子だけを調べることは今の技術ではなかなかできません。けれども（分子が）綺麗に並んでいれば、どんな性質を持っているかを調べることはできる。そのために結晶化して、その機能を調べることは今、盛んにやられているわけです。

　けれども、その結晶をつくることが難しい。数十年前、タンパクの結晶をつくるだけでノーベル賞を二つもらっているわけでしょう（※）。結晶ができたから、タンパクの二重らせんの構造がDNAであるとか、そういうことも調べられたことになったわけです。

※ジョン・ノースロップ（1891-1987,アメリカ）：1946年ノーベル化学賞受賞者「酵素の結晶化の発見」
※ウェンデル・スタンリー（1904-1871,アメリカ）：1946年ノーベル化学賞受賞者「酵素とウイルスタンパク質の結晶化」

　ちょっと横道に逸れた話になるけど、今、大きな結晶が必要ですよ。いろいろな結晶がありますが、大きな分子になると結晶をつくるのが非常に難しくなるのです。無理やりつくっても汚い結晶にしかならないわけね。

学問が加速度的に進歩するとき

　つまり何を言いたいかと言うと、結晶の形をコントロールする時、綺麗に方位を揃えて粒子を並べた方が良い時と、わざと乱してつくった方が良い時の両方がある、ということ。

―今までの話とどう関係するのですか？

　例えば金平糖みたいに、最初はいろいろな方位がランダムに並んでいる結晶ができていた。そして、その部分は硬いのだけども綺麗じゃないんです。先ほどの写真でも、結晶がランラムに並んでいる部分は黒っぽかったですね。

　でもツヤを出したい時、例えば印刷物でも同じように、表面をプラスチックでコーティングしますね。あれも二次元の結晶なんです。金平糖でもコーティングするために、最後に大きな結晶をつくってツヤを出す。

　このように（分子の）大きさではなく並び方をコントロールすることによって、いろいろな性質を出しているということ。そして、分子が大きなやつと小さなやつをいろいろ混ぜて使うと、とても多様なものができるでしょう、ということなんです。

　例えば、光沢や色をコントロールするために、結晶成長の知識を利用すると、ツヤを出したり、不透明にしたり、色を変えたり、いろいろ形や性質をコントロールすることができるんですよね。そして形のサイエンスは、これだけで話が済むわけではないんです。

　一つの極端な例としては、粒子サイズを大きくしてフォトニック結晶をつくる。すると、メノウやオパールなど非常に魅惑的でミステリアスな色をつくることなどができるでしょう。

　そして人間は、宝石としてそのようなものを使ってきたけれども、最近はその理由がわかってきて、それをうまく工業的に使おうという動きになっている、ということなんです。

　一つひとつがやっぱり、人間のあるところで一致するんですよね。例えば、昔からメノウやオパールは綺麗で神秘的だということで、宝石学が発達しました。

　一方、それとは全然別のところでコロイド結晶という学問が発達しました。それがあるところで、「あぁ、一緒だったんだね」と合体することによって、加速度的に学問が進歩する。まさに今、その時代だと思います。

　フォトニック結晶は、鉱物屋さんはなかなか知らないことかもしれません。なぜならば、電子デバイスなど工業的な分野でしか使われないからです。

　けれどもその分野で相当発達しているから、そういう知識をうまく取り入れることで、鉱物学もいろいろ発展するのだと僕は信じて疑わないんだよね。これからは、それをしなくちゃいけないと考えています。

いろいろな考えがだんだん整理され、一つの強いアイディアに結び付いていく

―前回のインタビューでも、「なぜだろう」という塚本さん個人の疑問が、いろいろな形でつながり広がっていき、発展していくプロセスを伺いました。塚本さんにとっては、それがごく自然なことなのですね。

　ごく自然な形だと思うよ。疑問があるからやっているだけで。別に金平糖って、鉱物や結晶学と関係ないと言えば関係ないよね。でもそれを調べることによって、また鉱物の形の原理がわかってくるんです。

　例えばここにガーネットの結晶があります。この結晶の中は割らなければどういう風になっているかがわからない。けれども、この形からすると「あぁ中はこうなっているのか」とある時、予測できるんです。なぜならば先ほどの金平糖のストーリーがあるからね。

　ところで、実はこのガーネット、レプリカなんですよ。昔オランダにいた時、本当の結晶の鋳型を取ってつくったプラスチック製のもの。この結晶を今、なぜ持ってきたかと言うと、金平糖とつながるんだよ。さきほどの結晶の外と中の話とは別にね。

　金平糖のツノが出る時、液滴があるところにくっつくからだ、と考えたわけですね。そのきっかけというのは、実はここからきているんですよ。ちょうどシャルル・ド・ゴール空港の話と同じで、きっかけは古いんだよ。

　なぜこのガーネットという結晶が、こんな面を持つかということを、昔、調べたことがあってね。結晶学的には、ある方位の面が出るはずだったの。でも、いくら観察しても出てこなかったんだよ。ここでも理論と実験の対比で違いがあったんです。

　では、なぜだろうか？と調べてみました。そこで、結晶というのは方向によって濡れ性が違う（異方性がある）から、濡れ性が良いところにしか液滴がつかないことを、このガーネットを通して学んだわけ。

　要するに、結晶の上に液がくっつくのに方位を選ぶんだ、ということ。つまり金平糖で、砂糖のカドのところに液がぺたっとくっつくのとほとんど共通するような話なわけ。

　このガーネットの研究をしていたから、金平糖がすぐにわかったわけね。考え方は違っても発想の仕方は、つながっているのです。そのようなものの組み合わせだから、できる話なのね。

―パリの空港で投影の仕方を知ったことからつながって、次に発展できた例と、ある意味で同じですね。

　うん。このガーネットの研究をやってなかったら、金平糖もわからなかったかもしれない。パリの空港で面白いと思っていなかったら、宇宙での"その場"観察もできなかったかもしれない。そのような一つ一つのことを大事にすべきだよね。

　いろいろな考えはあるかもしれないけど、それがだんだん整理されて、最終的に一つの強いアイディアに結び付いていく。結晶で例えるなら、小さな結晶がいっぱいでき始めて、それがだんだん整理されて、一つの大きな結晶にまとまってくる。研究って、そういうことじゃないかなと思っています。

―塚本さん、本日もありがとうございました。

▲このページのトップ ｜ HOME

コラボレーション

おすすめ記事

【特集】宮城の研究施設 一般公開特集

【特集】仙台市総合計画審議会 参加レポート 仙台の１０年をつくる

科学って、そもそもなんだろう？
最新５件

カテゴリ

• ■ 宮城の人々 (11)
• ■ 教育って、そもそもなんだろう？ (141)
• ■ 社会って、そもそもなんだろう？ (176)
• ■ 科学って、そもそもなんだろう？ (241)

取材先一覧

■ 幼・小・中学校

• ・みどりの森幼稚園 (1)
• ・めるへんの森幼稚園 (1)
• ・五橋中 (1)
• ・亘理町立長瀞小 (1)
• ・仙台青陵中等教育学校 (4)
• ・東六番丁小 (1)
• ・榴岡小 (2)
• ・聖ドミニコ学院 (9)

■ 高校

• ・仙台一高 (15)
• ・仙台二華 (14)
• ・仙台二高 (12)
• ・仙台城南高校 (5)
• ・仙台城南高等学校 (0)
• ・仙台高専 (4)
• ・宮城一高 (4)
• ・宮城県高等学校理科研究会 (2)
• ・岩ケ崎高 (1)
• ・東北工業大学高校 (0)

■ 大学

• ・名城大学 (1)
• ・山形大学 (1)
• ・岩手大学 (1)
• ・弘前大学 (1)
• ・東京工業大学 (1)
• ・東北大学 (184)
• ・東北学院大学 (4)
• ・東北工業大学 (5)

■ 国・独立行政法人

• ・内閣府 (1)
• ・宇宙航空研究開発機構 (5)
• ・文部科学省 (0)
• ・東北経済産業局 (17)
• ・水産総合研究センター東北区水産研究所 (1)
• ・理化学研究所 (3)
• ・産業技術総合研究所東北センター (36)
• ・科学技術振興機構 (1)
• ・防災科学技術研究所 (1)
• ・高エネルギー加速器研究機構 (1)

■ 自治体

• ・仙台市 (8)
• ・仙台市博物館 (4)
• ・仙台市天文台 (12)
• ・仙台市教育委員会 (13)
• ・仙台市産業振興事業団 (1)
• ・仙台市科学館 (8)
• ・仙台文学館 (2)
• ・仙台管区気象台 (2)
• ・塩釜市 (3)
• ・宮城県 (8)
• ・宮城県古川農業試験場 (2)
• ・宮城県教育委員会 (1)
• ・宮城県農業・園芸総合研究所 (1)
• ・気仙沼市 (1)
• ・登米市 (1)

■ 一般企業・団体

• ・DIC株式会社 (2)
• ・K sound design (1)
• ・KDDI (2)
• ・natural science (1)
• ・せんだい・みやぎＮＰＯセンター (2)
• ・てとてと (1)
• ・ひのき進学教室 (11)
• ・みやぎ工業会 (8)
• ・みやぎ工業会会長 (0)
• ・みやぎ産業振興機構 (3)
• ・アスター (1)
• ・インスペック (1)
• ・エツキ (1)
• ・ソニー (3)
• ・ソニー教育財団 (1)
• ・ソフトバンク (1)
• ・ティ・ディ・シー (1)
• ・デュナミス (1)
• ・ドットジェイピー (1)
• ・ナノテム (1)
• ・ハリウコミュニケーションズ (3)
• ・ハード工業有限会社 (1)
• ・フジイコーポレーション (1)
• ・プレファクト株式会社 (1)
• ・ヤマダフーズ (1)
• ・全国学習塾協会 (3)
• ・公益社団法人セーブ・ザ・チルドレン・ジャパン (1)
• ・勝山酒造部 (1)
• ・及源鋳造株式会社 (1)
• ・大武・ルート工業 (1)
• ・太白少年少女発明クラブ (1)
• ・宮城の新聞 (0)
• ・宮城県中小企業家同友会 (1)
• ・宮城県産業人クラブ (0)
• ・宮城県職業能力開発協会 (1)
• ・宮城県酒造組合 (2)
• ・工藤電機 (2)
• ・平孝酒造 (1)
• ・応用物理学会 (2)
• ・新東総業株式会社 (1)
• ・日刊工業新聞社 (7)
• ・日本アンドロイドの会 (1)
• ・日本技術士会 (2)
• ・日本私立大学団体連合会 (1)
• ・日本農芸化学会東北支部 (1)
• ・日本ＩＢＭ (3)
• ・日東イシダ (1)
• ・有限会社 柏崎青果 (1)
• ・東京エレクトロン宮城 (1)
• ・東北ニュービジネス協議会 (1)
• ・東北活性化研究センター (3)
• ・東北経済連合会 (1)
• ・東北電力 (2)
• ・東北電子産業株式会社 (1)
• ・東栄科学産業 (1)
• ・林精器製造 (1)
• ・株式会社三栄機械 (1)
• ・株式会社悠心 (1)
• ・河北新報 (1)
• ・神田産業株式会社 (1)
• ・秋田化学工業 (1)
• ・笹氣出版印刷 (1)
• ・米鶴酒造 (1)
• ・萩野酒造 (1)
• ・農芸化学会 (1)
• ・遠藤工業 (1)
• ・鈴木製作所 (1)
• ・阿部蒲鉾 (1)
• ・阿部蒲鉾店 (1)
• ・鳴子の米プロジェクト (1)
• ・ＮＥＣトーキン (1)